口胡系列……
题目描述
小 Y 是一个爱好旅行的 OIer。她来到 X 国,打算将各个城市都玩一遍。
小Y了解到, X国的 n 个城市之间有 m 条双向道路。每条双向道路连接两个城市。 不存在两条连接同一对城市的道路,也不存在一条连接一个城市和它本身的道路。并且, 从任意一个城市出发,通过这些道路都可以到达任意一个其他城市。小 Y 只能通过这些 道路从一个城市前往另一个城市。
小 Y 的旅行方案是这样的:任意选定一个城市作为起点,然后从起点开始,每次可 以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问该 城市时经过的道路后退到上一个城市。当小 Y 回到起点时,她可以选择结束这次旅行或 继续旅行。需要注意的是,小 Y 要求在旅行方案中,每个城市都被访问到。
为了让自己的旅行更有意义,小 Y 决定在每到达一个新的城市(包括起点)时,将 它的编号记录下来。她知道这样会形成一个长度为 n 的序列。她希望这个序列的字典序 最小,你能帮帮她吗? 对于两个长度均为 n 的序列 A 和 B,当且仅当存在一个正整数 x,满足以下条件时, 我们说序列 A 的字典序小于 B。
- 对于任意正整数 ,序列 A 的第 i 个元素 和序列 B 的第 i 个元素 相同。
- 序列 A 的第 x 个元素的值小于序列 B 的第 x 个元素的值。
[戳]( https://www.luogu.org/problem/P5022 )
Solve
题意看似复杂,其实很显然。
首先让我们面向数据编程。
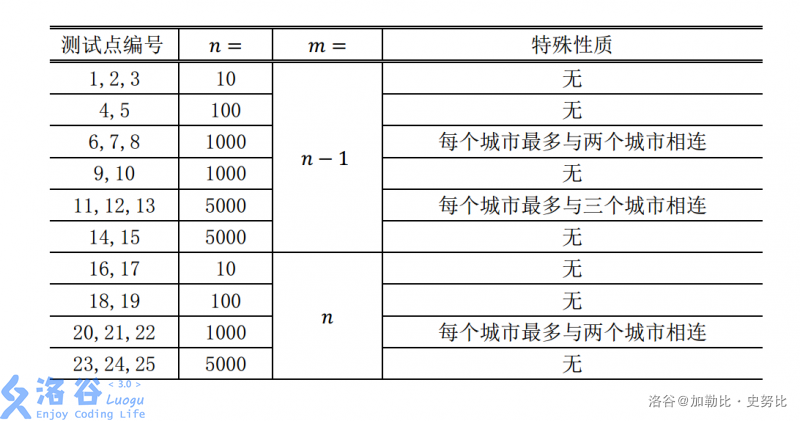
m=n-1
当m=n-1时,图也就变成了一棵树
也就是这个亚子的。
(滑稽
那么小Y所要求的旅行方案就是这棵树字典序最小的DFS序。
字典序最小是题目要求的,不解释,那为什么是DFS呢?
每次可 以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问该 城市时经过的道路后退到上一个城市
你难道不觉得这很像DFS的遍历方式吗。
当你已经确定一个节点为下一个遍历目标的时候,你就一定要遍历完他的子树,否则一旦回溯,就再也回不来了。
反过来,DFS序就不用多解释了。如何遍历才能做到字典序最小呢?首先肯定要从节点1开始,否则直接输在起跑线上。然后呢?按照节点编号从小到大直接遍历就珂以了。
进一步说,如何保证从小到大的遍历顺序呢?如果你用邻接矩阵的话,请随意。如果是邻接表的话,排个序就行了。真的。
首先保证边(u,v)中,。
以u为第一关键字,v为第二关键字。从大到小排序。因为剖析邻接表的本质,存的边,相对于存进来时的边,他是倒序的。这样就保证了按照邻接表遍历的时候,是从小到大遍历的。
这也是我做这道题时,口胡的一种做法,应该对。
然后,我们可以那到60分的好成绩,然而加上D1T1T2还是够不上SD的分数线
m=n
当m=n时。
猜猜这叫什么,还是树。

(滑稽
但是他换了个名字,叫基环树,其实也就是树上多了个环。因为m=n。那该怎么做呢?我们之前有了树上的做法,所以我们可以把他变成树来做。一条边的事。
找环然后挨个删边,暴力。
找环的话就自己想想叭,挺简单的。
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 500001
using namespace std;
int n,m,ans[N],res[N],txt,num1,num2;
int head[N],len;
int st[N],cnt;
bool vis[N],fis[N];
struct node{
int to,nxt,r;
}eg[N*2];
struct note{
int u,v;
}d[N*2];
bool cmp(const note a,const note b){
if(a.u!=b.u) return a.u>b.u;
else return a.v>b.v;
}
void add(int u,int v,int w){
len++;
eg[len].to=v;
eg[len].r=w;
eg[len].nxt=head[u];
head[u]=len;
}
void find_ring(int u,int fa){//vis是否在环里,fis是否遍历过,eg[].r为边的编号
fis[u]=true;
for(int i=head[u];i;i=eg[i].nxt){
int v=eg[i].to;
if(eg[i].r!=fa&&fis[v]&&txt==0){
vis[u]=true;
txt=v;
}
else if(eg[i].r!=fa&&!fis[v]){
find_ring(v,eg[i].r);
if(vis[v]) vis[u]=true;
}
}
if(vis[u]) st[++cnt]=u;
if(u==txt) vis[u]=false;
}
void dfs(int u,int fa){
res[++txt]=u;
for(int i=head[u];i;i=eg[i].nxt){
int v=eg[i].to;
if((u==num1&&v==num2)||(v==num1&&u==num2)) continue;
if(v==fa) continue;
dfs(v,u);
}
}
void new_ans()
{
if(ans[1]==0){
for(int i=1;i<=n;i++) ans[i]=res[i];
return ;
}
for(int i=1;i<=n;i++){
if(res[i]>ans[i]) break;
if(res[i]<ans[i]){
for(int j=i;j<=n;j++) ans[j]=res[j];
return ;
}
}
return ;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++) {
scanf("%d%d",&d[i].u,&d[i].v);
if(d[i].u>d[i].v) swap(d[i].u,d[i].v);
}
sort(d+1,d+1+m,cmp);
for(int i=1;i<=m;i++) add(d[i].u,d[i].v,i),add(d[i].v,d[i].u,i);
if(m==n-1){
dfs(1,1);
for(int i=1;i<=n;i++) printf("%d ",res[i]);
}
else{
find_ring(1,-1);
for(int i=1;i<=cnt;i++){
txt=0;
if(i==cnt) num1=st[cnt],num2=st[1];
else num1=st[i],num2=st[i+1];
dfs(1,1);
new_ans();
}
for(int i=1;i<=n;i++) printf("%d ",ans[i]);
}
return 0;
}
后言
这个找环也是我之前做一道基环树题时口胡的做法。所以这篇题解珂以说是口胡系列。