其实所有内容都是我们可爱的学姐lcr教授的，我只是借用了一下而已。~~话说学OI的竟然还有学姐。~~不知道为什么我的部分LaTeX废了，所以只能抠图了。

gcd

用(a, b)表示gcd(a, b)

(a, b) = (b, a % b)

(a, b) = (b, a - b) (a > b)

exgcd

求解ax + by = gcd(a, b)

void exgcd(int a, int b, int &g, int &x, int &y)
{
	if (!b) { x = 1; y = 0; g = a; return; }
	exgcd(b, a % b, g, y, x), y -= (a / b) * x;
}

证明：

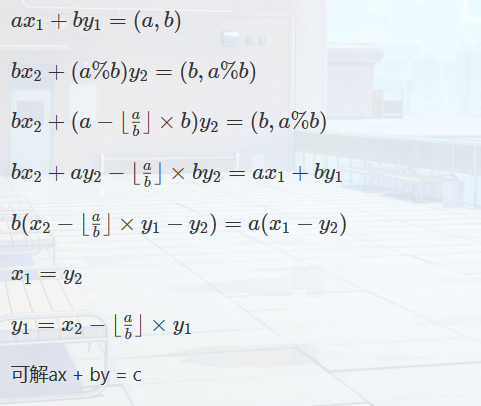
裴蜀定理

方程 ax + by = c 有解的充要条件是gcd(a, b)是c的因数

费马小定理

p为质数且a不是p的倍数时，$a ^ {p - 1}= 1\pmod p$

欧拉定理

a和m互质时，$a ^ { \phi(m)} = 1 \pmod m$ 即$a ^ c = a^{ c\ mod\ \phi(m)} \pmod m$

a和m不互质时，$a ^ c = a^{ c\ mod\ \phi(m) + \phi(m)} \pmod m$ (c > $\phi(m)$)

线性筛

素数，欧拉函数，莫比乌斯函数，约数个数

求逆元

模数为质数 ksm(a, p - 2)

exgcd

线性求逆元 inv[i] = mod - (mod / i) * inv[mod % i]

推导

设t = mod / i， k = mod % i

-t * i == k (% mod)

-t * inv[k] = inv[i] (% mod)

inv[i] = mod - (mod / i) * inv[mod % i] (% mod)

中国剩余定理

int CRT()
{
    int ans = 0, M = 1, x, y;
    for (int i = 1; i <= k; i++) M *= m[i];
    for (int i = 1; i <= k; i++)
    {
        int tp = M / m[i];
        exgcd(tp,b[i],x,y);
        x = get_inv(tp, m[i])
        ans = (ans + tp * x * a[i]) % M;
    }
    return (ans + M) % M;
}

求组合数

C(n, m)

递推，预处理阶乘+O(1)